Définition

\(\triangleright\) Définition d'un champ éléctrostatique

En considérant deux points A et B de charges \(q_1\) et \(q_2\), la force de A sur B est donnée par la Loi de Coulomb:
$$\underset{A\to B} {\vec F}=q_B\times\frac 1{4\pi\varepsilon_0}\frac{q_A}{r^2}\vec e_r=q_B\times\vec E_A$$
\(\vec E\): champ électrostatique créé par la charge \(q_A\) (en volt/mètre)
Le champ éléctrostatique est un Champ vectoriel et peut être vu comme une propriété locale de l'espace.

Topologie-Symétrie

\(\triangleright\) Notion utile

Graphe - Surface
Ligne de niveau

Champ créé par une charge ponctuelle

Grâce à l'équation du champ éléctrostatique \(\vec E=\frac{q\vec u_r}{4\pi\epsilon_0r^2}\), on peut tracer les lignes de champ
On observe:

Champ créé par un doublet

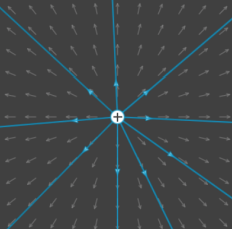
Considérons deux charges ponctuelles de signe opposé. C'est ce qu'on appelle un doublet éléctrostatique.
Les lignes de champ partent de la charge positive à la négative:



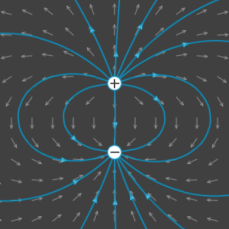
On observe ici un plan de symétrie et un plan d'antisymétrie (en raison du signe opposé)

Champ crée par deux charges de même signe

Considérons deux charges de même signe et de valeur différente situé sur un axe horizontal.



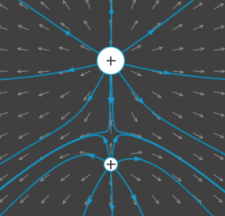
Les lignes partent également des charges positives.
Un plan de symétrie est également présent mais pas de plan d'antisymétrie.
On observe également un point ou le champ est nul appelé point sigulier

Remarque

Si \(q_A\lt 0\), le champ \(\vec E_A\) est centripète
Si \(q_A\gt 0\), le champ \(\vec E_A\) est centrifuge
Plus on s'éloigne, plus \(\vec E_A\) est petit
La plus petite charge possible est \(1,6\times 10^{-19}\;\mathrm C\)
\(1\;\mathrm C\) est une charge énorme